AOC23 - 8 December
Good morning, today I will have to be a quick session, since the rest of the day is allocated teaching python to my girlfriend. And she is as closely affiliated to computer technology as I am to gardening. And have you seen any posts about plants here? Me neither.
But from the looks of it today is a mild puzzle. Famous last words. So let's get to it.
The puzzle boils done to:
- A list of nodes (Tuples) with a "left" and "right" entry each containing the name of the next node
- You start at 'AAA' and need to reach 'ZZZ'
- At the start of the input is an infinitely repeating sequence of "L" (left) and "R" (right) instructions that you have to follow, until you hit a "ZZZ"
- I need to count the steps to reach "ZZZ"
Learning from yesterday, I will have another read over it, before we start.
Ok, no, that really seems to cover everything.
I think I am going to use a dictionary for quick indexing of the nodes, a left and right type.
I will definitely not repeat RL infinitely, because as far as I have seen from day 5 elm is not lazy.
solve1 : String -> Int
solve1 str =
parse str |>
traverseNodes |>
List.length |>
type alias Binode = (String, String)
type Direction = Left | Right
type alias Map =
{ instructions : List Direction
, nodes : Dict String Binode
}
parse : String -> Map
traverseNodes : Map -> List String
This is our main Data types and involved functions.
Parsing
To parse I am going to split the long instruction first, and map the string to a list of directions. Then I am going through step by step and assign the left side of the assignment as key and the right side as value as a tuple.
parse : String -> Map
parse str =
let
(firstRow, nodeRows) = halfOn "\n\n" str
parseDirection c =
case c of
'L' -> Just Left
'R' -> Just Right
_ -> Nothing
parseNode = listOfRegex "\\w+" >> toPair "" >> Tuple.mapSecond String.trim
in
{ instructions =
String.toList firstRow |>
List.map parseDirection |>
Maybe.values
, nodes =
String.lines nodeRows |>
List.map (halfOn "=" >> (Tuple.mapBoth String.trim parseNode)) |>
Dict.fromList
}
Traversing the Nodes
traverseNodes : Map -> Maybe (List String)
traverseNodes map =
let
follow dir = if dir == Left then Tuple.first else Tuple.second
findNode dir =
Maybe.andThen
(\node ->
Maybe.andThen
(\found -> Just <| follow dir found)
(Dict.get node map.nodes))
collect ins mnodes =
Maybe.andThen (\nodes ->
let
nextNode dir = findNode dir (List.head nodes)
in
case ins of
dir::rem ->
Maybe.andThen
(\a ->
case a of
"ZZZ" -> Just <| a :: nodes
_ -> Maybe.andThen
(\remaining_nodes -> Just <| remaining_nodes)
(collect (if rem /= []
then rem else map.instructions) <| Just (a :: nodes))
) <| (nextNode dir)
_ -> Nothing
) mnodes
in collect map.instructions (Just ["AAA"])
This is my solution. Please be advised that there is more concise ways in other languages, but I am trying to follow the most idiomatic path, using as many language unique features as possible. I modeled the function in the Maybe type to get some practice.
So, my follow function maps Left to "firs"t and Right to "second" value of the Node, findNode gets the next node for direction, these are used in collect to recursively go over the node list until it finds "ZZZ", when it runs out of instructions it starts with the full instruction list from scratch. I implemented this mostly with pattern matching. If it should encounter any edge case it returns Nothing and jumps out. I think this is quite elegant and resiliant.
Here I ran the algorithm against the output:
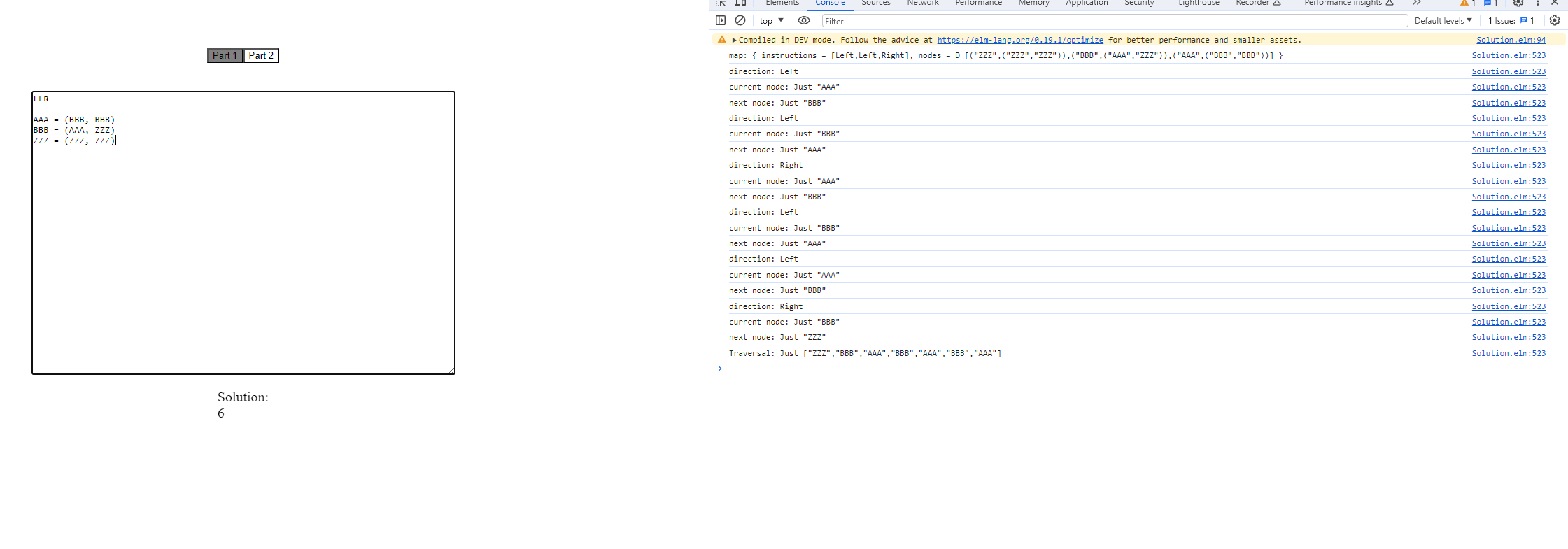
Now let's try with the full data

I already anticipated this. I think this is the brother of Day 5's OOM Exception.
Now it's time to freshen up my recursion knowledge. I was aware and pretty sure that I implemented my algorithm as a tail recursion, aka loop-like recursion. So I should not have a stack overflow because of nested calls. But I suspect that we have a halting problem, that it can't find an exit on Z. And now that I think of it, this thing is essentially a turing tape. We have a little turing machine (minus the state changes through writing) here.
I am gonna do some research into this.
Let's debug it. I am going to print out the length of the remaining instructions and check how often they repeat.
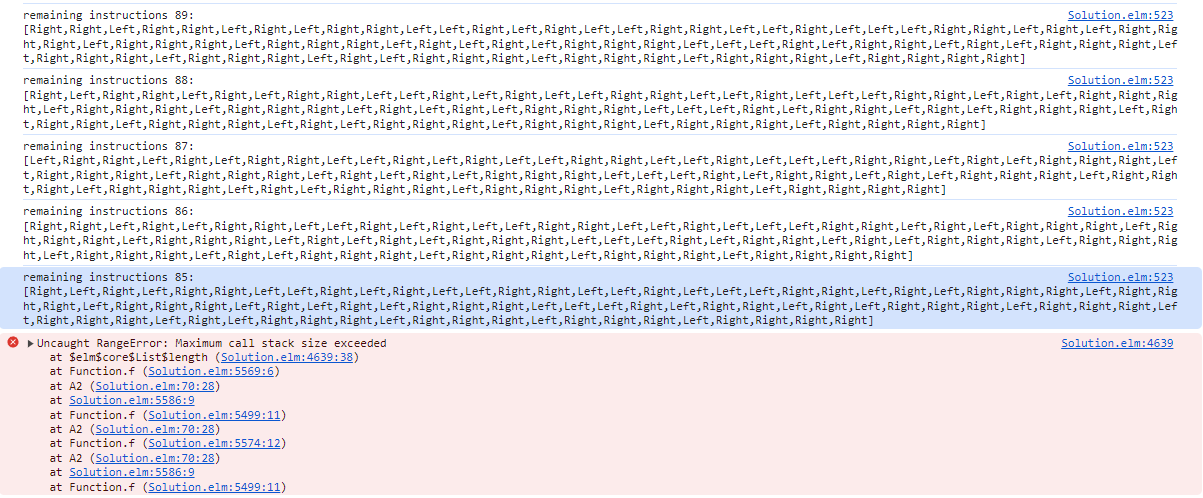
This is frightening, I merely called the function 100+ times. This seems to be a limitation of elm. Fortunately after a quick browse I found a library who is supposedly taking care of this problem.
recurse : (a -> Result b a) -> a -> b
even : Int -> Bool
even =
recurse <| \n ->
evenStep n `Result.andThen` oddStep
odd : Int -> Bool
odd =
recurse <| \n ->
oddStep n `Result.andThen` evenStep
Ok, so we have ourselves a function that defines the recursive part as step that either returns "Ok function call" or "Err and result". Tried to install it, but it seems to be very outdated and incompatible with my core libraries.
I have an idea. I could model this part:
case ins of
dir::rem ->
Maybe.andThen
(\a ->
case a of
"ZZZ" -> Just <| a :: nodes
_ -> Maybe.andThen
(\remaining_nodes -> Just <| remaining_nodes)
(collect (if rem /= []
then rem else map.instructions) <| Just (a :: nodes))
) <| (nextNode dir)
_ -> Nothing
As a List.fold and only call the function again, once it is done without a match.
Let's do that. No wait. When I use fold for the instruction set, I can not guarantee that the folding stops in the middle of the instruction set. So I would be wasting computation cycles eventho I already found the solution. So I have to do more research about alternative control flow options. But the loop library seems to have the answer.
whileJust : (a -> Maybe a) -> a -> a
-- example
f : Int -> Maybe Int
f n =
if n < 15
then Just (n + 5)
else Nothing
We have already most of the type work already done in our function. So let's try refactoring it to match this construct.
traverseNodes : Map -> List String
traverseNodes map =
let
follow dir = if dir == Left then Tuple.first else Tuple.second
findNode dir =
Maybe.andThen
(\node ->
Maybe.andThen
(\found -> Just <| follow dir found)
(Dict.get node map.nodes))
collect traversalData =
let
nextNode dir = findNode dir (List.head nodes)
(ins, nodes) = traversalData
in
case ins of
dir::rem ->
Maybe.andThen
(\a ->
case a of
"ZZZ" -> Nothing
_ -> Just
(if rem /= []
then rem
else map.instructions, a :: nodes)
) <| (nextNode dir)
_ -> Nothing
in
Tuple.pair map.instructions ["AAA"] |>
whileJust collect |>
Tuple.second
This was easier than I thought, and I have to say I like it even more than the incompatible libraries solution, giving us an approximate "while" loop semantically. Using the notion of the Maybe type as loop mechanism is borderline genius in terms of idiomacy and elegance.
Very happy with this solution.

And would you know it. It was the right solution. Nice!
Let's see what curve ball is thrown to us this time in Part 2
Part 2
And what a curve ball that is... So If I understood it right:
- We need to start on every node that ends with "A", so pattern "\w+A"
- Follow each pattern till we end of "\w+Z", it does not specify if they should be unique entries
- But assume that it is the case because the A nodes match in Number with the Z node
I think this will best solved with parallelism. I have a general hunch that Elm uses the type Task for asynchronous operations, and there is this parallelism library which allows us to execute Tasks in parallel.
This is the function that we need:
attemptList :
{ tasks : List (Task x a)
, onUpdates : ListMsg a -> msg
, onSuccess : List a -> msg
, onFailure : x -> msg
}
-> ( ListState msg a, Cmd msg )
Takes a record with the tasks and some callback functions and produces a ListState msg, Cmd msg Tuple. Hm... I will have to look into them now. Ok so Task's type constructor needs two values a failed value and successfull value.
Also a task is just the description. A task is to be executed (similar in concept of how a class is a blueprint for an object, but an object needs to be instanced). Execution modes are perform and attempt. These both return the Type 'Cmd', hm interesting. So maybe I should look into that.
the only way to do real parallelism is with
Cmd.batch
There is no parallelism. This is due to the JS virtual-machine in the browser.
So after doing that small research, I learned two things. Real parallelism is a lie in Javascript, so no performance gain really. And the Task and therefore Cmd run into Elm's blackbox and need to be handled by updating the top-level model directly which goes against how I setup and want my general framework and setup to work.
With this little detour out of the way I will now run them in sequence and pray. My first instinct would be to map the filtered nodes with A but that could potentially lead to OOM again if every entry is mapped to a gigantic list of nodes, so I will use folding right off the bat.
solve2 : String -> Int
solve2 str =
let
map = parse str
in
map.nodes |>
Dict.keys |>
List.filter
( Regex.contains
(Regex.fromString "\\w+A" |>
Maybe.withDefault Regex.never)
) |>
List.foldl
( \a b ->
b + (traverseNodes a map |> List.length)
) 0
So this time we refactor traverse node to match different cases as arguments so we can reuse it. Filter the keys of the map for every entry that ends with A and fold over it after each iteration into the total count.
But I misunderstood the prompt, and will have to refactor again a bit.
- I have to traverse at the same time from each node to the next (using the same direction for every single node). I can only stop, if all the runs end up on a node ending with Z, meaning if one run reaches Z but the others don't, I have to continue. Oh boy. That changes things quite dramatically.
improve output format
traverseNodesSim : Regex.Regex -> Map -> List String -> List String
traverseNodesSim dest map entries =
Tuple.pair map.instructions (List.map (List.singleton >> Just) entries) |>
whileJust
(\traversalData ->
let
(ins, listOfTraversals) = traversalData
in
case ins of
dir::rem ->
let
runs =
listOfTraversals |>
List.map (\run ->
run |> Maybe.andThen
(\valid_run ->
(nextNode map.nodes (List.head valid_run) dir) |>
Maybe.andThen
(\node -> Just <| node :: valid_run)
)
)
result =
runs |>
Maybe.values |>
List.map
(\run -> List.head run |>
Maybe.withDefault "" |>
Regex.contains dest) |>
List.all identity
in
if
result
then Nothing
else Just (if rem /= [] then rem else map.instructions, runs)
_ -> Nothing) |>
Tuple.second |>
Maybe.values |>
List.head |>
Maybe.withDefault []
Well I started running this. But didn't have a result since 5 min. After 15 min. It ran out of memory. Because I am keeping track of all the nodes, wanting to do it similarly to part 1.
I need to refactor it accordingly.
(\traversalData ->
let
(ins, lastNodes, count) = traversalData
in
case ins of
dir::rem ->
let
nodes =
lastNodes |>
List.map
(\node ->
Maybe.andThen
(\valid_node ->
(nextNode map.nodes (Just valid_node) dir) |> -- (Debug.log "This node" <| )
Maybe.andThen Just
) node)
result =
nodes |>
Maybe.values |>
List.map (Regex.contains dest) |>
List.all identity
in
-- Debug.log ("(" ++ Debug.toString (List.length rem) ++ ")" ++ " " ++ Debug.toString dir ++ "\n\n")
-- (
if
result
then Nothing
else Just (if rem /= [] then rem else map.instructions, nodes, count + 1)
Let's run this again. After 30 min. my webpage disintergrated. So I decided to stop for today.
On Reddit I have read something about observing the data behavior to identify a recurrence in the pattern which would reveal itself as a certain category of problems (Nondeterministic finite automaton) solvable by a certain approach (LCM). Problem a. I am learning a new language (so mostly I have to debug errors that are created by my inexperience with it and research most of the core functionality, like with the recursion problem) and Problem b. even if I were to recognize some of the patterns, my computer science vocabulary is very limited, and how does the saying go? You can't search for something, you don't know, you have to search for.
(Sorry for the short rant but) This is similar to the reason that I started hating chess. In the beginning when you learn the game you feel like creativity and intuition (when coming up with move combinations and tactics) are the key. But the more and more advanced you get you start seeing recurring patterns. And instead of being able to solve problems yourself you study existing solutions. Leading to a convergence of play styles. Creativity and intuition is replaced by sheer knowledge and experience. And that is somewhat sad.
Takeaway
I need the courage to refactor sooner and commit to it more decisively. This was a problem of levels of abstraction and interfacing, which of course are one of the core ideas behind the Part 2. (Aswell as challenging your general knowledge of certain problem domains and applying them to optimize solutions.) Functions build abstraction spaces. I tend to try to write functions in terms of one size that fits all, but here I had to dissolve one function into an anonymous function which I then copy pasted in the alternative implementation. But that is ok, since they cover two completely different implementations that solve the same problem with two separate specifications. And as such can have diverging internal implementation sharing most of the lower level functionality. To express this in terms of our problem domain, they are both the same number, but just have a different primary factorization (learned this concept from my research into LCM). I am happy that my algorithm could at least resolve the test input on part 2 and call that a small win.
But I definitely learned a lesson today (and this is all I wanted). Often a problem is so complex, that just implementing the necessary steps to reproduce the solution is not enough. When encountering algorithms with this complexity we then need to observe the behavior/output and based of these observations find mathematically or algorithmic shortcuts. I completely overlooked and doubted (honestly) that the random string of left and right instructions would be recurrent within themselves, and it also never occured to me to check for this behavior in my output. This requires knowledge and experience to identify common categories of problems and the existing solutions for them.
From now on I will only tackle part 1, and part 2 only if I have spare time. Debugging, researching and these time consuming observations take up almost my entire day.
See you on the next challenge